Coarse
Semantic Segmentation with Multiscale Dimensionality Reduced Subblocks
https://drive.google.com/file/d/1RIiajKYdxFUbOvZvl42x1kssDJFxO6dv/view?usp=sharing
Motivation
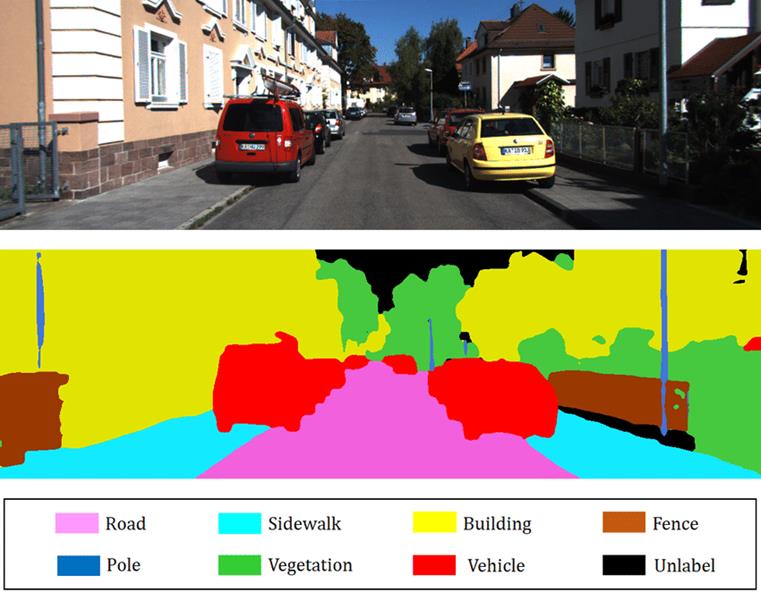
The semantic segmentation task.
The typical goal of semantic
segmentation is to assign each pixel in an image to one of a few semantic
classes. In the example shown here, each region of the image of a street is
labeled as a road, sidewalk, cat, building etc. Oftentimes this problem is
reduced to finding a binary pixel mask for each of the possible classes (is
this pixel part of a car, or not?), then combining these class-wise masks into
a single semantic map.
Applications of semantic segmentation.
Semantic Segmentation has a wide
array of applications in many industries, and is an important intermediate step
in creating truly intelligent computer-vision systems. In the context of
self-driving vehicles, knowing where roads, pedestrians, and other objects are
in a single image is a necessary step to determine where these objects are in
3D space. Semantic segmentation is also used in medical image analysis in order
to determine the locations of tumors and other defects.
Unfortunately, generalized semantic
segmentation is among the hardest computer vision tasks because to predict the
class of any single pixel requires high level of contextual knowledge about
that pixel and its surroundings. There is almost no
way to predict the semantic class of a single pixel using only its RGB values
directly. A Blue-Greyish pixel could be part of a sky, a road, a building, a
car, a road, or a jacket. It's the challenge of semantic segmentation combined
with the clear utility that has us interested in the task.
Current State of the Art
UNET
Our Approach
Motivation
A major challenge of semantic
segmentation, or any other machine learning techniques in computer vision is
the curse of dimensionality. For a modestly-sized 480x360 color image, there
are 480 * 360 * 3 = 518,400 values to consider (one for each RGB value of each
pixel). And for semantic segmentation, the output is of size 480 * 360 =
172,800 per class. To train neural
networks with data of this dimensionality requires a vast amount of training
data and computational power, which are both expensive.
In
short, the goal of our approach is to create a learning-based approach to
semantic segmentation that creates a "smaller" predictive model than current
convolutional methods. This in turn reduces the amount of training data
required to train the model, and speeds up the learning process. This is done
by dramatically reducing the dimensionality of the input to our predictive model.
Multiscale Sliding Windows
One way that we accomplish this is
by creating a model that makes a prediction only about a small "chunk" of an
image. In our case, we predict the semantic composition of only a 32x32 chunk
of a high-resolution image. However, in order to make a prediction about that
small chunk, it helps to also know the visual "context" of the area surrounding
that chunk. This context is captured by using a multiscale "pyramid" of
progressively larger but lower-fidelity chunks surrounding the "core" chunk we
wish to make a prediction on.

In
order to perform semantic segmentation on the whole image, we then slide this
pyramid across the whole image, giving us a semantic prediction of every 32x32
subblock.
Texture Dimensionality Reduction with PCA
As mentioned, image data is
inherently very high-dimensional.
Limiting the prediction inputs to the images of the multiscale pyramid helps
reduce this dimensionality somewhat, but not enough to make a truly small model.
So, we use Principle Component Analysis to reduce the input dimensionality even
further.
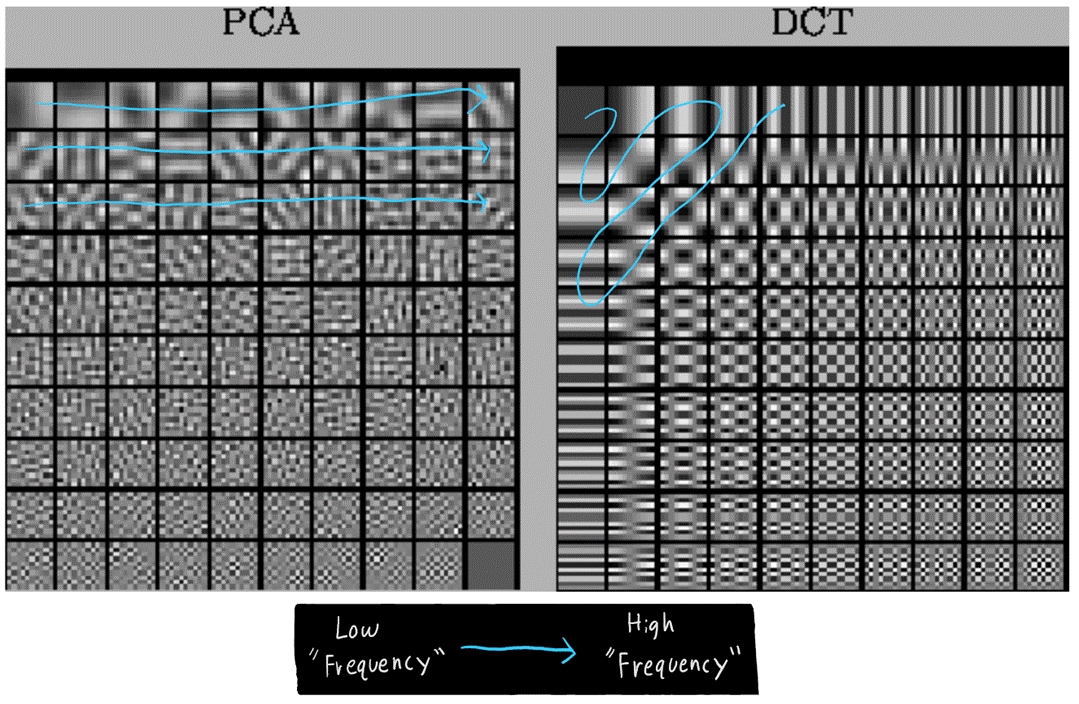
Consider a single 32x32 black &
while image. Similar to how we can use the fourier
transform / discrete cosine transform to perform a "basis" transformation, giving
us the original 32x32 image in different basis coefficients, we can also use
PCA to get different basis coefficients for the image. We can then "drop" most
of these basis coefficients, obtaining a compact "representation" of the
original 32x32 image. If we want to perform a prediction about this 32x32
image, we can use maybe 90 of the most important PCA coefficients instead of
the whole 1024 pixel values.
Color Dimensionality Reduction with PCA
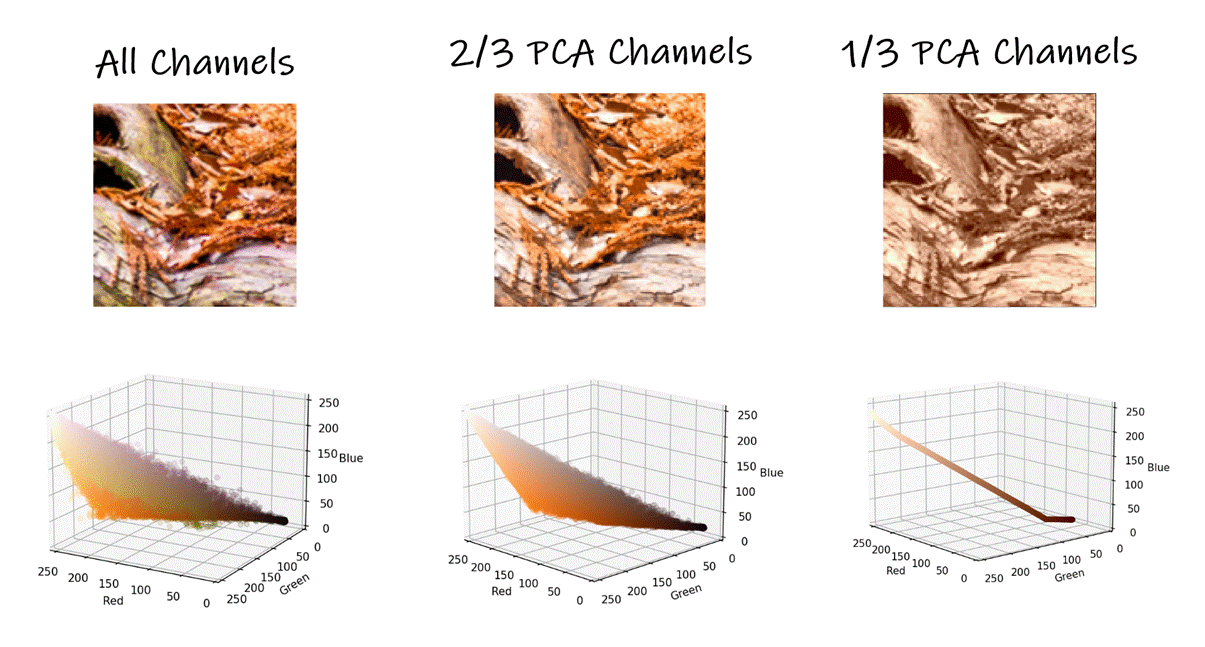
Beyond using PCA to reduce the
dimensionality of the "Texture" information of an image sub-block, we can also
use PCA to reduce the dimensionality of the color information of each image.
Images are typically thought of as having red, green, and blue channels. To dimensionality-reduce
an image, we could apply the PCA texture encoding to the red, green, & blue
channels of an image. However, if you apply PCA to the RGB values of an image,
you get a more efficient way to represent an image. You get three new channels,
specific to that image, where the first channel is "most important", the second
one less important than the first channel, and the last channel least
important. For example, this small image of some tree roots with mulch is well
approximated when using only ⅔ "PCA" channels.
Instead
of applying PCA texture dimensionality reduction to the red, green, and blue
channels, we apply it to the 3 custom "PCA" channels. Because we know that the
channels are ordered by importance, we encode the most texture information
about the first channel, and less in the other two channels.

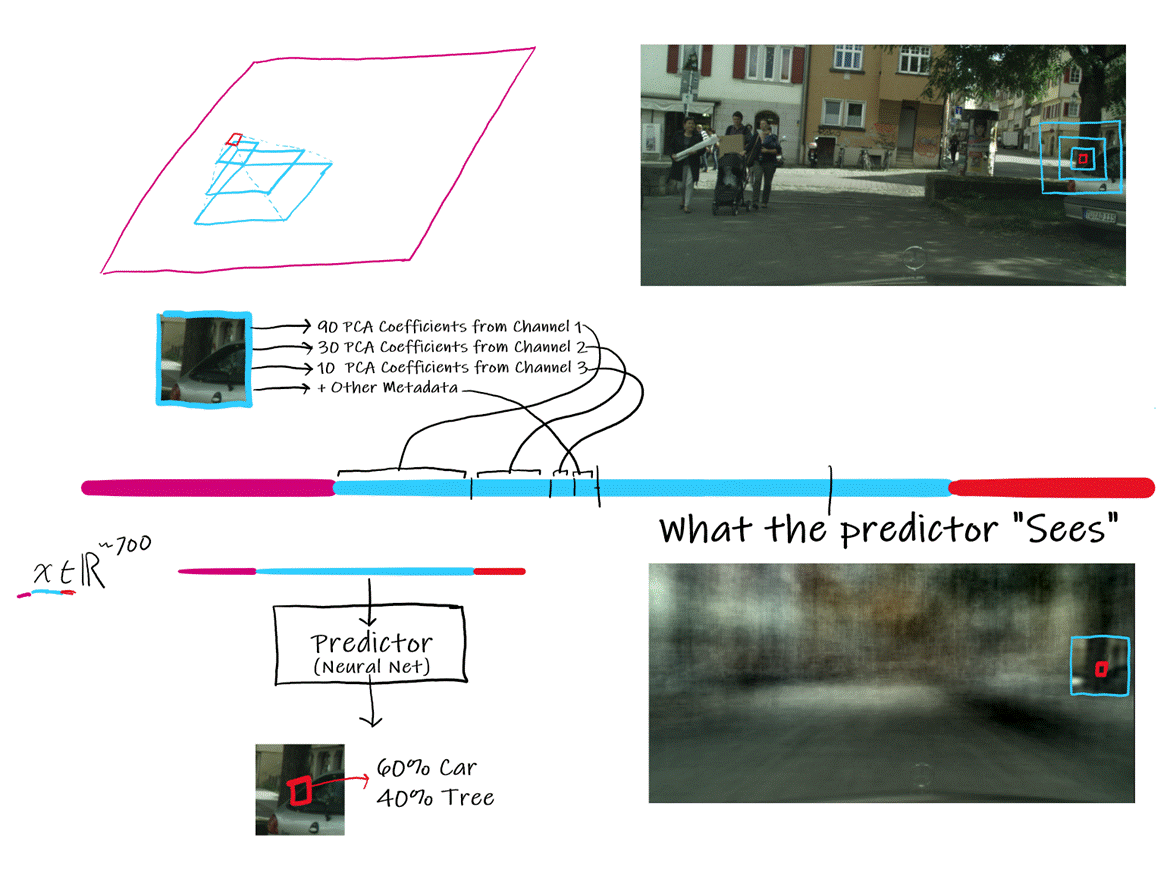
Putting it together: the encoding.
In order to predict the semantic
composition of a single "core" block, we encode the visual information of that
block, and larger blocks in that multiscale pyrymic
into a single vector, reducing the dimensionality of the input by a large
margin.

Task
Cityscapes Dataset
Utilize the cityscapes dataset to
classify objects within the city, such as cars, foliage, sky, road, and signs.
Our inspiration for using this being self-driving cars.
Constraints
No corners for now. Also we just
predict the semantic composition of a core block, not which pixels actually
belong to which class.
Results
Model Size
Our model size contains a total of
47,998 parameters, which is tiny in comparison to UNET's massive 2,060,424
parameters in their model.
Training Time
Given this massive difference in the
number of parameters, the training times are also vastly different. Our neural
network could be trained within 20 minutes while utilizing 30% of a laptop
processor, meanwhile UNET's pixel-wise segmentation model used a graphics card
while still taking 400 minutes to train.
Inference/ Prediction Time
At this moment, it takes 60 seconds in order to process and predict the labels on the image.
Accuracy
The accuracy of our 47,998 parameter
model has an accuracy of 82.79%. Our 203,630 parameter model has an accuracy of
90.08%, and our 845,982 has an accuracy of 93.04%. Each model was only trained
for 20 minutes.
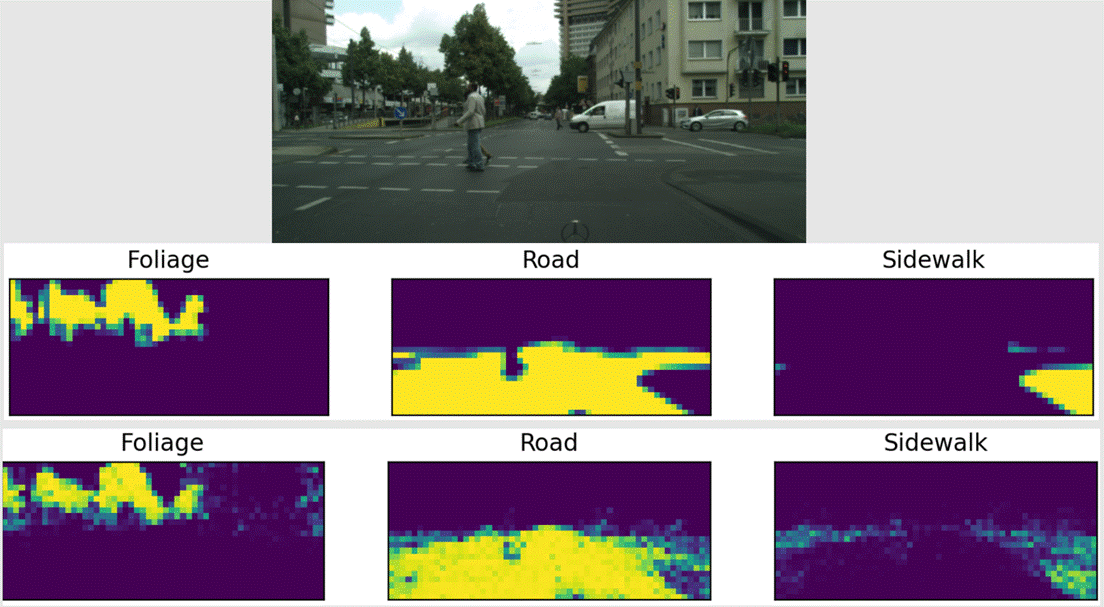
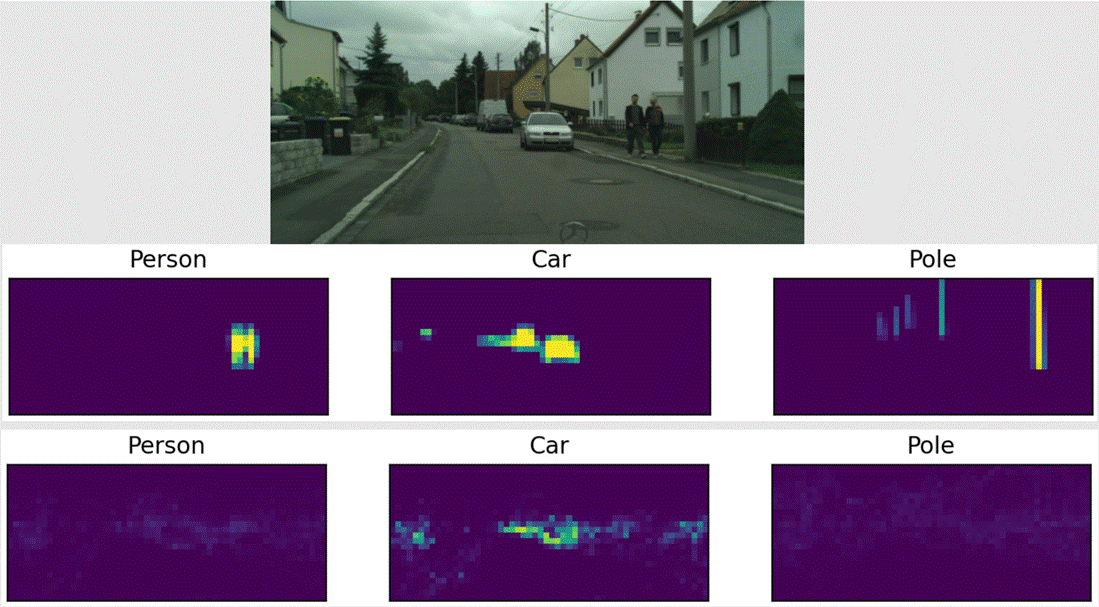
The pictures below are examples of
the model in action using the 47,998 parameter model, with the top three being
the actual labels taken from the image, and the bottom three being the ones our
model had predicted.
Successes:
Areas of improvement:
Future Work
Inference Time is slow
Inference time is slow with it taking 60
seconds to predict all of the labels within the large image.
Corners
We want our method of image segmentation
to also work on corners, at this moment it cannot reach the corners due to the
lack of information received from our current algorithm.
Follow Up with a coarse -> fine step.
We would like to refine our coarse
segmentation to a pixel-wise, fine segmentation as to have more data to work
with. Having the coarse segmentation limits our ability to have a completely
accurate prediction due to losing some fine information which is important at
times.
References
●
The cityscapes dataset
○
Cordts, M., Omran, M., Ramos, S., Rehfeld, T., Enzweiler,
M., Benenson, R., ... & Schiele, B. (2016). The cityscapes dataset for
semantic urban scene understanding. In
Proceedings
of the IEEE conference on computer vision and pattern recognition
(pp.
3213-3223).
●
PCA color reduction
○
De Lathauwer, L., &
Vandewalle, J. (2004). Dimensionality reduction in higher-order signal
processing and rank-(R1, R2,…, RN) reduction in multilinear algebra. Linear Algebra and its Applications, 391, 31-55.
●
CNNs:
○
LeCun
, Y., Haffner, P., Bottou, L.,
& Bengio, Y. (1999). Object recognition with
gradient-based learning. In
Shape,
contour and grouping in computer vision
(pp. 319-345). Springer, Berlin,
Heidelberg.
●
UNET:
○
Ronneberger
, O., Fischer, P., & Brox, T. (2015, October). U-net:
Convolutional networks for biomedical image segmentation. In
International Conference on Medical image
computing and computer-assisted intervention
(pp. 234-241). Springer, Cham.
●
ClidingWindow
, then CNN:
○
Vigueras-Guillén, J. P., Sari, B., Goes, S. F., Lemij, H.
G., van Rooij, J., Vermeer, K. A., & van Vliet,
L. J. (2019). Fully convolutional architecture vs sliding-window CNN for
corneal endothelium cell segmentation.
BMC
Biomedical Engineering
, 1(1),
1-16.
Link to GitHub repo:
https://github.com/benthehuman1/UW-Vision-Segmentation